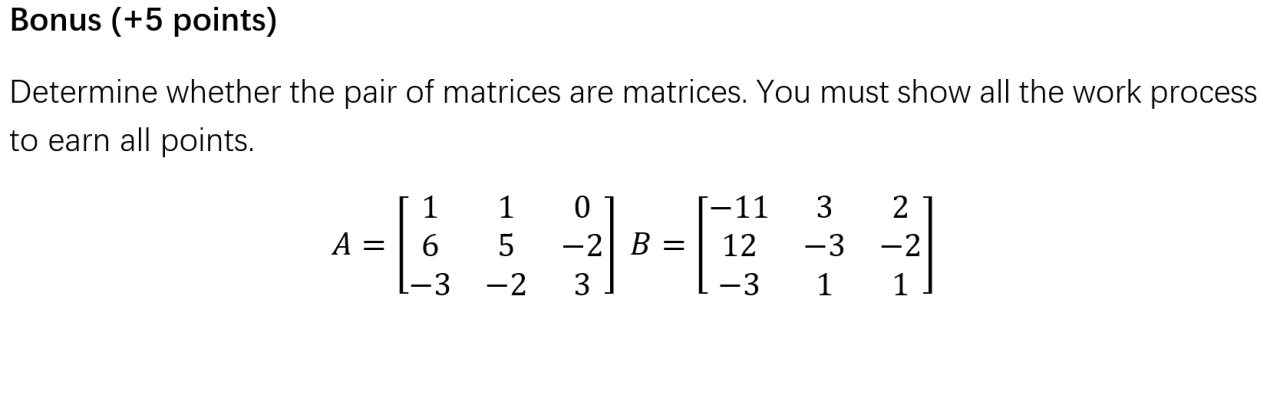Embark on a captivating journey into the realm of determinants and inverses with our Determinants and Inverses Quiz Part 1. This quiz is meticulously crafted to test your comprehension of these fundamental matrix concepts and equip you with the skills to tackle complex mathematical problems.
As you navigate through this quiz, you will delve into the intricacies of matrix determinants, exploring their properties and applications. You will also encounter the concept of matrix inverses, uncovering their significance and methods of computation. Prepare to engage with challenging problems that will push your understanding and solidify your knowledge.
Determinants and Inverses: Determinants And Inverses Quiz Part 1

Determinants and inverses are fundamental concepts in linear algebra with wide-ranging applications in mathematics, engineering, and other fields. This article provides an overview of these concepts, including their definitions, methods for calculation, and applications.
Determinants, Determinants and inverses quiz part 1
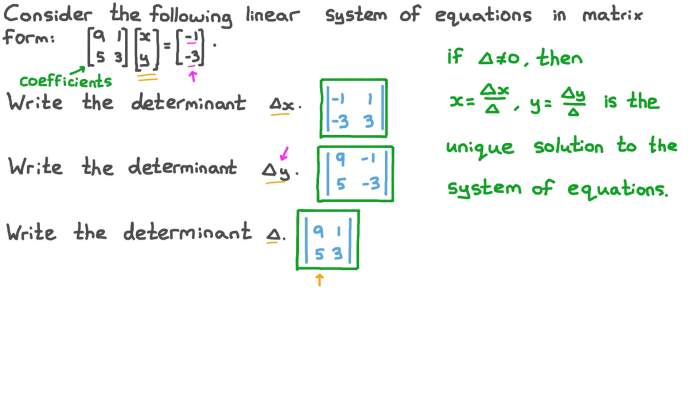
The determinant of a matrix is a scalar value that captures certain properties of the matrix. It can be used to determine the matrix’s invertibility, solvability of systems of linear equations, and the area or volume of geometric figures.
To calculate the determinant of a matrix, various methods can be employed, such as cofactor expansion, row/column operations, or the Laplace expansion.
Inverses
The inverse of a matrix, if it exists, is a unique matrix that, when multiplied by the original matrix, results in the identity matrix. The inverse of a matrix can be used to solve systems of linear equations, find eigenvalues and eigenvectors, and perform other matrix operations.
A matrix has an inverse if and only if its determinant is nonzero. The adjoint matrix, row/column operations, or the Gauss-Jordan elimination method can be used to find the inverse of a matrix.
Relationship between Determinants and Inverses
The determinant of a matrix and its inverse are closely related. The determinant of a matrix is equal to the product of the matrix’s eigenvalues. If the determinant is nonzero, the matrix has an inverse, and the inverse can be computed by dividing the adjoint matrix by the determinant.
Applications of Determinants and Inverses
Determinants and inverses have numerous applications in various fields.
- Solving systems of linear equations: Determinants can be used to determine whether a system of linear equations has a unique solution, multiple solutions, or no solutions.
- Area and volume calculations: Determinants can be used to find the area of a parallelogram or triangle and the volume of a parallelepiped.
- Linear algebra operations: Inverses are used in matrix transformations, finding eigenvalues and eigenvectors, and solving matrix equations.
Quick FAQs
What is the significance of a matrix determinant?
A matrix determinant provides valuable information about a matrix. It can indicate whether a matrix is invertible, singular, or orthogonal. Additionally, determinants play a crucial role in solving systems of linear equations and calculating geometric properties like area and volume.
Under what conditions does a matrix have an inverse?
A matrix has an inverse if and only if its determinant is nonzero. A matrix with a zero determinant is considered singular and does not possess an inverse.
How can I efficiently find the inverse of a matrix?
There are several methods to find the inverse of a matrix, including the adjoint matrix method, row/column operations, and the Gauss-Jordan elimination. The choice of method depends on the size and properties of the matrix.